My research is in Topological Data Analysis (TDA) and its applications to biological data. I am part of Dr. Bubenik’s research group. TDA is a field that studies the shape of data with the complex topological structure using tools from algebraic topology.

Below are the projects that I am/was working on:

Topological data analysis of C. elegans locomotion and behavior

This is the joint project with Ashleigh Thomas, Alex Elchesen, Peter Bubenik and biologists from Georgia Tech Kathleen Bates and Hang Lu. The published version of this project is available here.

We apply topological data analysis to the behavior of C. elegans, a widely studied model organism in biology. In particular, we use topology to produce a quantitative summary of complex behavior which may be applied to high-throughput data. Our methods allow us to distinguish and classify videos from various environmental conditions and we analyze the trade-off between accuracy and interpretability. Furthermore, we present a novel technique for visualizing the outputs of our analysis in terms of the input. Specifically, we use representative cycles of persistent homology to produce synthetic videos of stereotypical behaviors.

Topological and metric properties of spaces of generalized persistence diagrams

This paper is currently under revision and the preprint is available here.

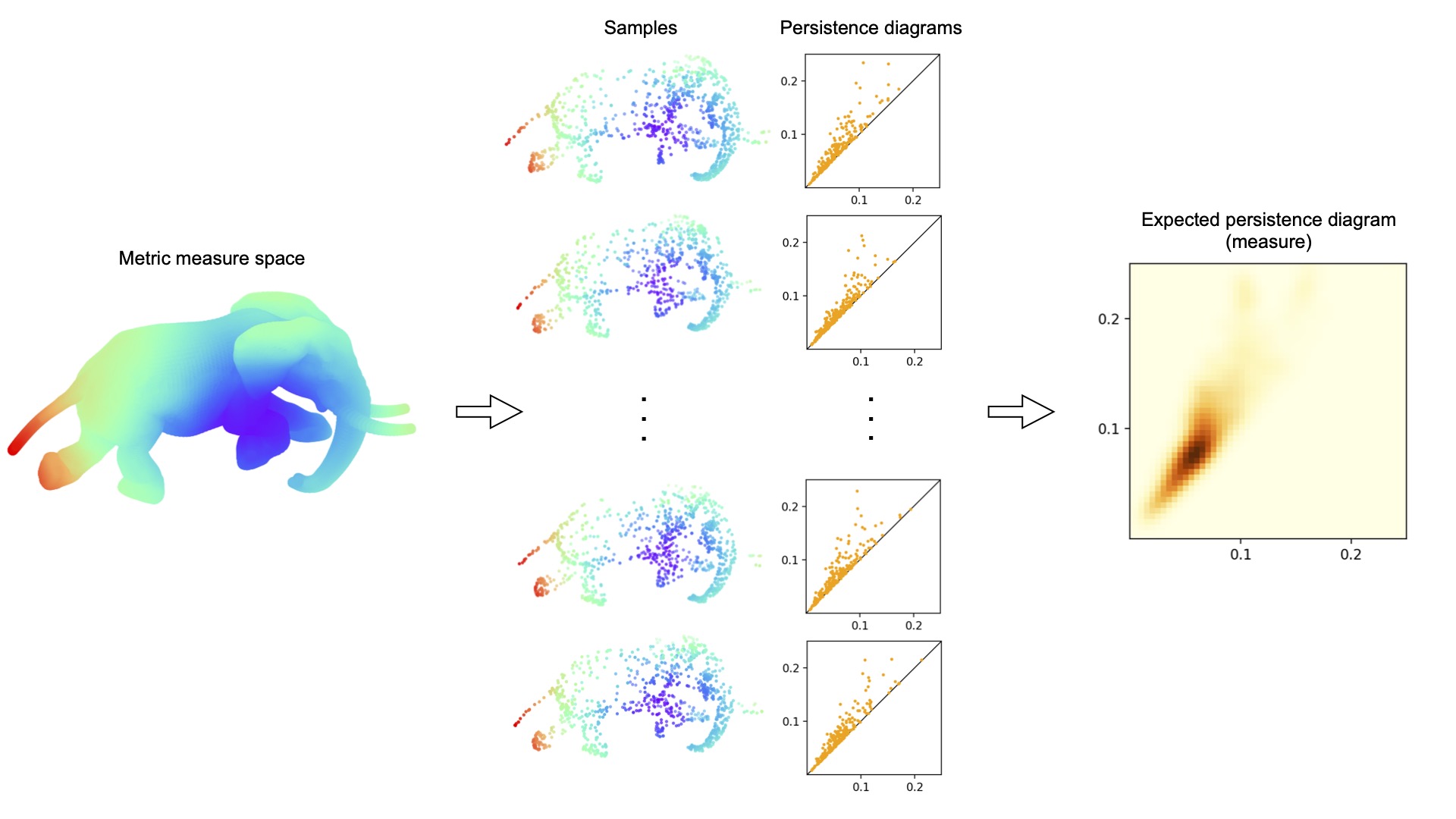
Motivated by persistent homology and topological data analysis, we consider formal sums on a metric space with a distinguished subset. These formal sums, which we call persistence diagrams, have a canonical 1-parameter family of metrics called Wasserstein distances. We study the topological and metric properties of these spaces. Some of our results are new even in the case of persistence diagrams on the half-plane. Under mild conditions, no persistence diagram has a compact neighborhood. If the underlying metric space is σ-compact then so is the space of persistence diagrams. However, under mild conditions, the space of persistence diagrams is not hemicompact and the space of functions from this space to a topological space is not metrizable. Spaces of persistence diagrams inherit completeness and separability from the underlying metric space. Some spaces of persistence diagrams inherit being path connected, being a length space, and being a geodesic space, but others do not. We give criteria for a set of persistence diagrams to be totally bounded and relatively compact. We also study the curvature and dimension of spaces of persistence diagrams and their embeddability into a Hilbert space. As an important technical step, which is of independent interest, we give necessary and sufficient conditions for the existence of optimal matchings of persistence diagrams.

 

Learning on persistence diagrams as Radon measures

This is the joint project with Alex Elchesen, Jose Perea, and Tatum Rask. The preprint is available here.

Persistence diagrams are common descriptors of the topological structure of data appearing in various classification and regression tasks. They can be generalized to Radon measures supported on the birth-death plane and endowed with an optimal transport distance. Examples of such measures are expectations of probability distributions on the space of persistence diagrams. In this paper, we develop methods for approximating continuous functions on the space of Radon measures supported on the birth-death plane, as well as their utilization in supervised learning tasks. Indeed, we show that any continuous function defined on a compact subset of the space of such measures (e.g., a classifier or regressor) can be approximated arbitrarily well by polynomial combinations of features computed using a continuous compactly supported function on the birth-death plane (a template). We provide insights into the structure of relatively compact subsets of the space of Radon measures, and test our approximation methodology on various data sets and supervised learning tasks.

 

Topological data analysis of pattern formation of human induced pluripotent stem cell colonies

This is the ongoing joint project with Eunbi Park, Jack Toppen, Elena Dimitrova, Melissa Kemp, Peter Bubenik, and Daniel Cruz. The recent poster on this project is available here.

Human induced pluripotent stem cells (hiPSCs) have the potential to self-renew and the ability to differentiate into any cell of a human body. We extracted cell-specific signal intensities from confocal microscopy images, assigned cell types based on respective intensities, and studied changes in cell pattern formations among cell types through topological data analysis. In particular, we detected differences in the spatial organization of stem cells based on different biological markers, which gave us insight into the strength of their neighbor-to-neighbor signaling. Also, we quantified changes in the cell pattern formations of hiPSC colonies during their differentiation. Furthermore, the pipeline we have developed is general-purpose and can be applied to various microscopy images.