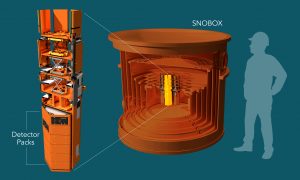

SuperCDMS detectors are designed with the primary function of detecting the minute crystal lattice vibrations (phonons) and ionization (charge) generated within the detector crystal by elastic collisions between detector nuclei and as low-mass dark matter particles. The energy deposited in a detector by an interacting dark matter particle may be as low as a few tens of electron volts (eV). Event detection at such energy levels requires a sensitive experimental apparatus. The foremost requirement is that the detector be maintained at a very low temperature to distinguish the deposited energy from the thermal energy of the detectors nuclei.
The detectors require state-of-the-art thin film superconducting technology. Each of the germanium and silicon crystals (measuring 100 mm in diameter and 33 mm thick) have roughly 1000 sensors deposited on both faces of the detector. The phonon sensors consist of an array of tiny superconducting transition edge sensors which themselves consist of microscopic strips of tungsten coupled to aluminum “fins” to collect phonon energy from the crystal. Some of the detectors also collect ionization signals with a small voltage applied across the crystal while others convert the ionization to phonons using a much larger applied voltage.
Transition Edge Sensors
One technique used for measuring energy is calorimetry. The energy absorbed by a physical system with heat capacity C (the calorimeter) causes an increase in temperature according to the following equation:
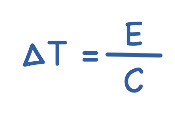

Since the energies of interest in the Dark Matter and x-ray detection fields are on the order of 10 keV (~ 1fJ), using of calorimeters with C as low as ~ 1 pJ/K, results in a temperature change of ~ 1 mK. This illustrates the need for highly sensitive thermometers.
An accurate method of measuring temperature involves using resistive thermometer to transform the temperature change into a voltage signal, based on the following circuit.
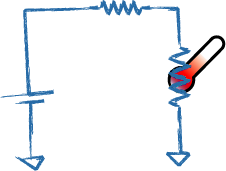
By applying a voltage bias across a temperature sensitive resistor and measuring the current flowing through the circuit we can detect any temperature changes. In order to be sensitive to truly minute temperature variation, however, the dependence of the resistance on temperature, R(T) must be quite large. This dependence is quantified by the variable alpha, which is defined as
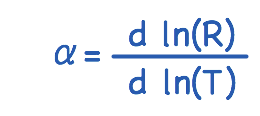
Superconductors are well known for having zero resistance below a certain “critical temperature” (Tc), while above this temperature they have a normal state resistance that is characteristic of the metals of which they’re made.
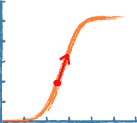
Within the span of ~ 1 mK around the Tc, the resistance rises from zero to its normal value, resulting in a large value of alpha, and thus a strong dependence of R on T, as shown in this figure. When some energy is absorbed in the device, the temperature and resistance quickly increase,
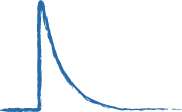
eventually the device cools back down to the ambient temperature, accompanied by a decrease in resistance. This produces a pulse whose amplitude is a good measure of the absorbed energy.