My research group focuses on the development, numerical simulation, and analysis of mathematical models of biological systems and their validation and calibration against experimental data.
We primarily study cell migration in various contexts such as embryonic development and tumor growth.
See below for short descriptions of some of our current and former projects, and see Publications for more details.
Early Embryonic Development
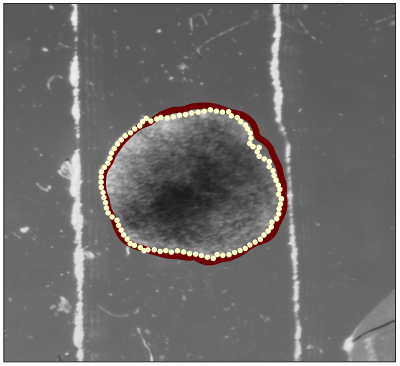
Gastrulation is an early phase of embryonic development in which the germ layers of the embryo are formed, each of which eventually gives rise to distinct tissues and organs. Our group studies continuum mechanical models of cell migration to compare to experimental data, for which we have developed an automated method of extracting data from time-lapse sequences of images. This allows for examination of the mechanical forces that drive cell migration during gastrulation in the aquatic frog Xenopus laevis.
Eye Development
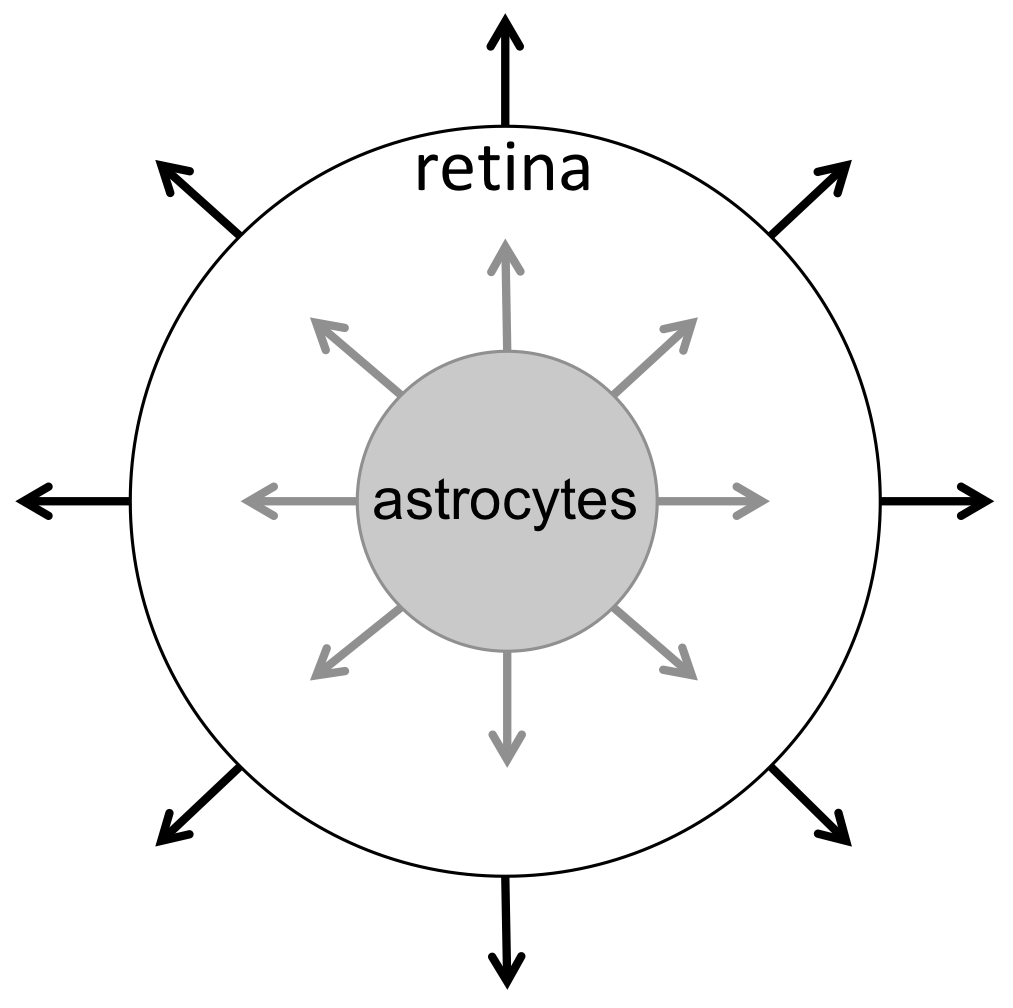
Retinal blood vessels are essential for adequate oxygen supply to the inner layers of the retina, the light sensitive tissue in the eye. During development of the eye, formation of the retinal vasculature via angiogenesis is critically dependent on prior establishment of a mesh of astrocytes, which are a type of brain glial cell. Our group studies continuum models of astrocyte migration that incorporate the essential mechanisms of astrocyte spread and maturation during retinal embryonic development. We compare various model fits to data and analyze the existence and shapes of traveling wave solutions.
Wound Healing
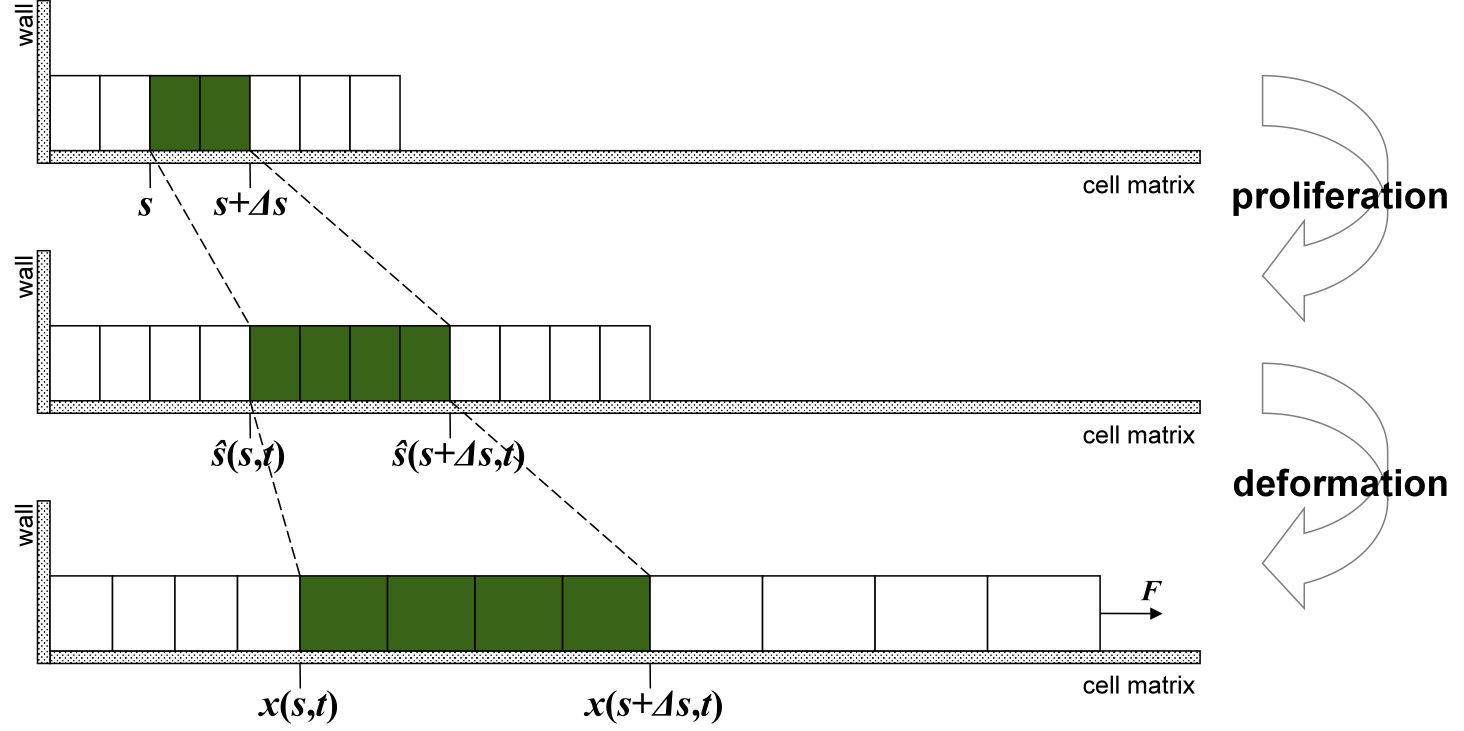
Necrotizing enterocolitis (NEC) is an intestinal inflammatory disease that is a major cause of death in premature infants and is characterized by the impairment in the ability of intestinal epithelial cells to move effectively. Our group studies continuum mechanical models of cell layer migration, and different types of mathematical solutions are analyzed for existence and uniqueness. When there is cell proliferation in the model equations, traveling wave solutions exist. When there is no cell proliferation, similarity under scaling solutions exist.
Brain Cancer
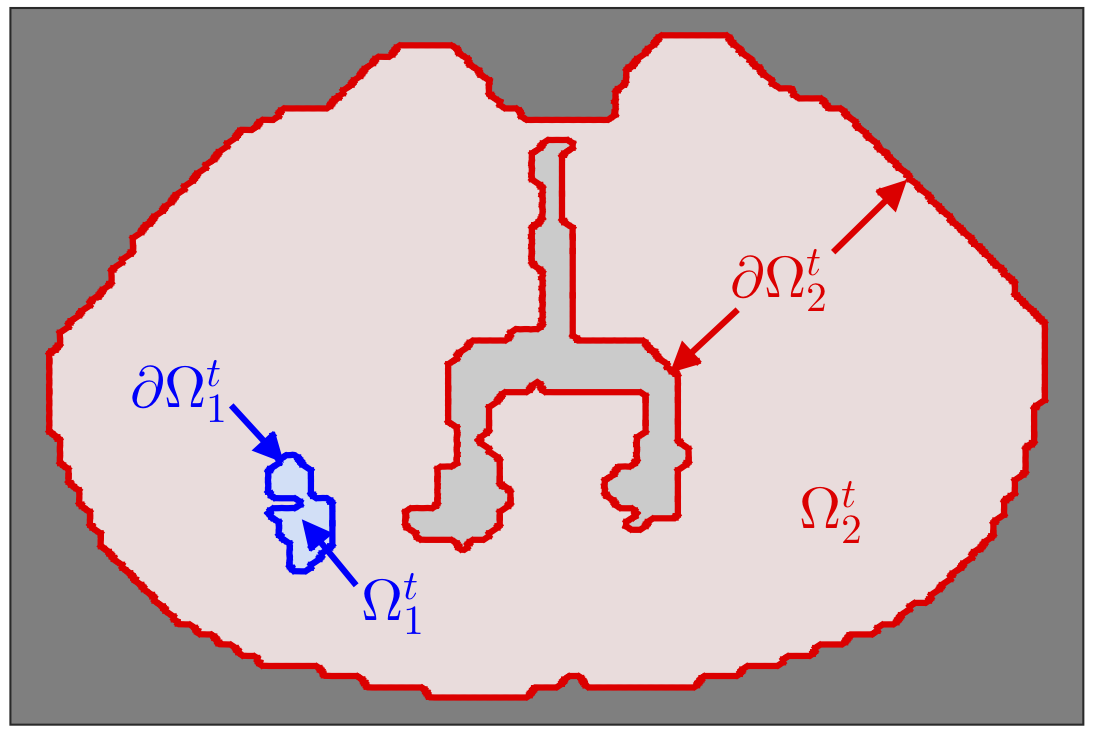
Glioblastoma multiforme (GBM) is the most common and most deadly primary brain tumor in adults and it is characteristically highly diffusive and proliferative. Our group studies mathematical models of in vitro and in vivo glioma tumor growth with and without treatment in comparison with experimental data. We also study traveling wave solutions of the mathematical equations.
Entomology
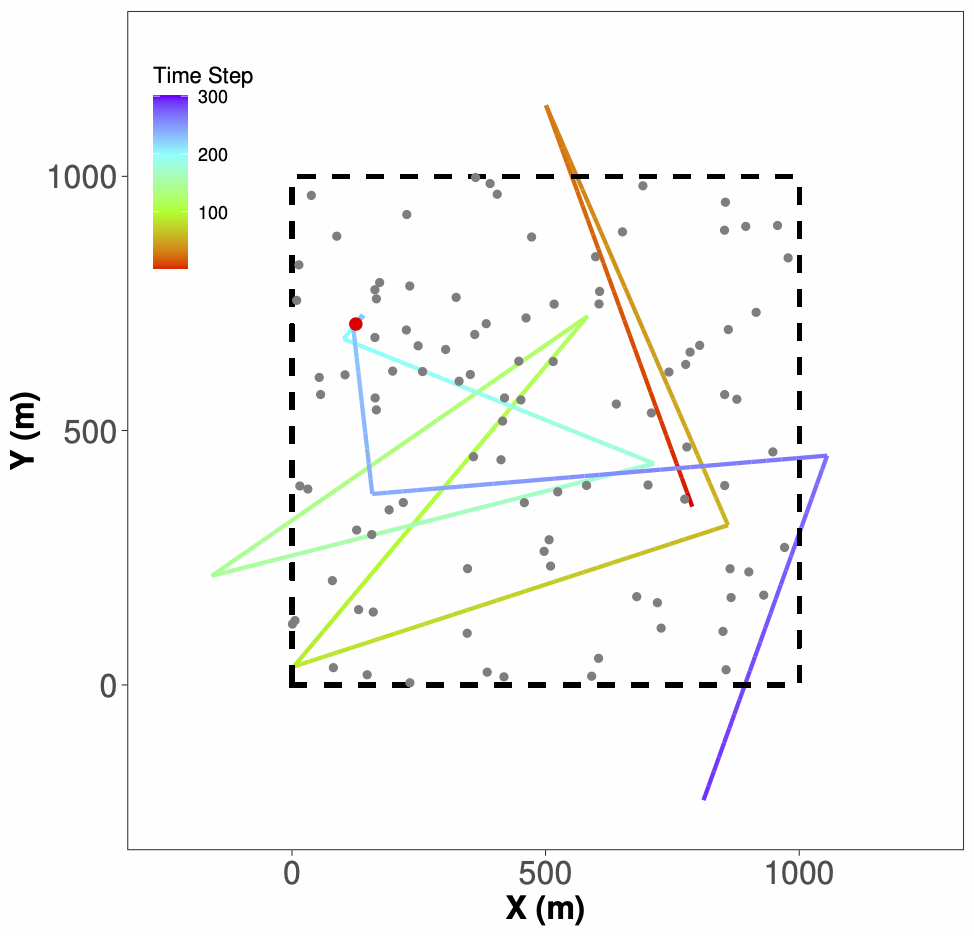
Understanding the mating dynamics and movement of insects can inform strategies for disease management. Our group has studied agent-based and continuum models of moth mating and blue tongue spread via biting midges. We’ve determined characteristics of female pheromone release for mating success and have used sensitivity analysis to identify factors that would play a significant role in future blue tongue disease outbreaks.
Population Dynamics
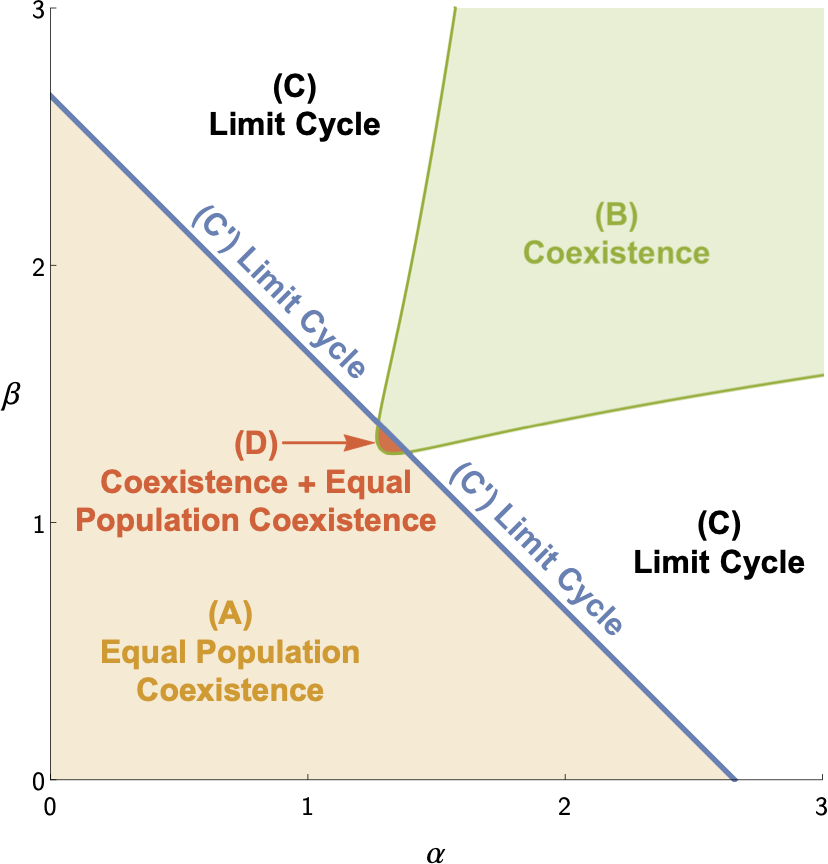
The May-Leonard model was introduced to examine the behavior of three competing populations. Our group studied a perturbation of the system by adding the capability of global mutations, allowing one species to evolve to the other two in a linear manner. Using bifurcation and stability analysis, we found that the model has a richer variety of fixed points but no longer exhibits nonperiodic cyclic solutions.
Kidney Hemodynamics
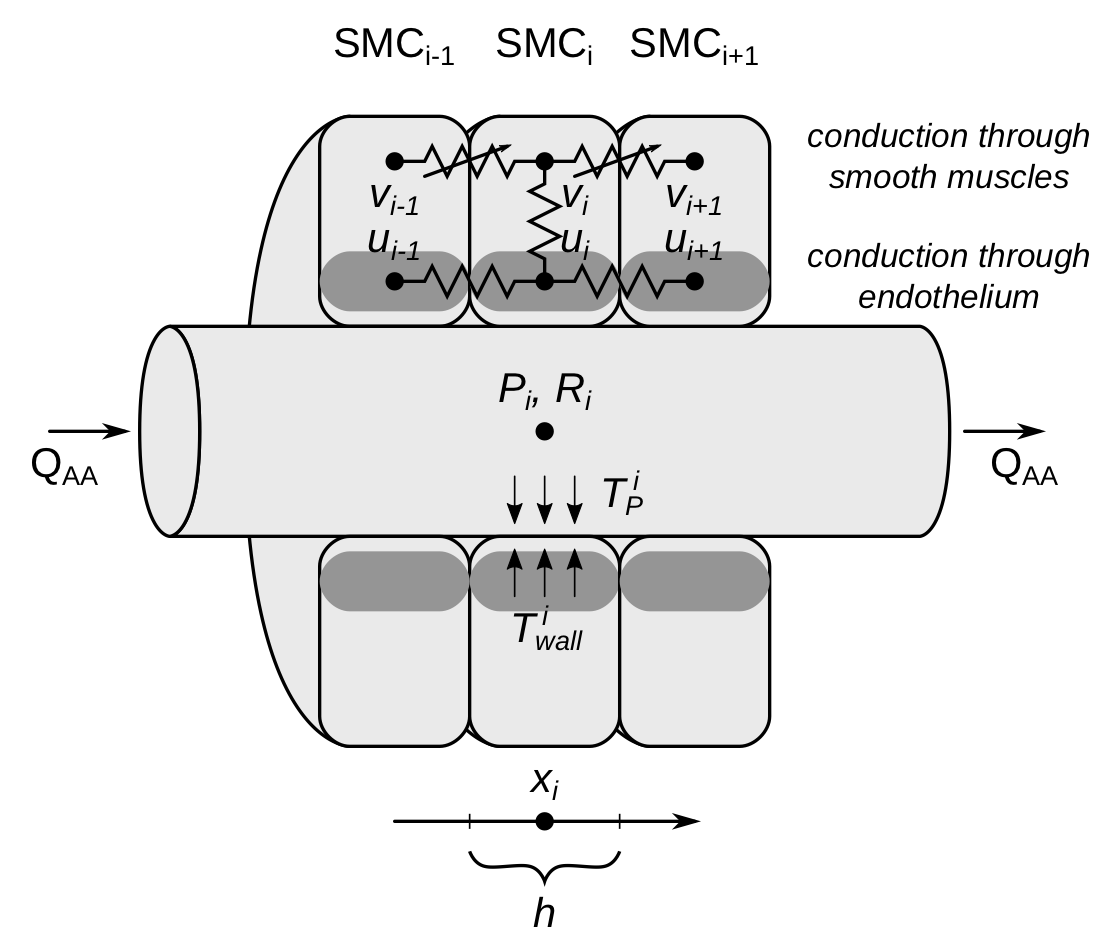
Autoregulation in the kidney is an adaptive process which is important in maintaining a constant glomerular filtration rate despite changes in blood pressure or metabolism. One type of renal autoregulation is the myogenic response of the afferent arteriole, the blood vessel that delivers blood to the kidney’s filter. Our group has studied a multicellular model of the kidney afferent arteriole where models of single smooth muscle cells are connected through gap junctions and presented with blood flow.
Data Mining
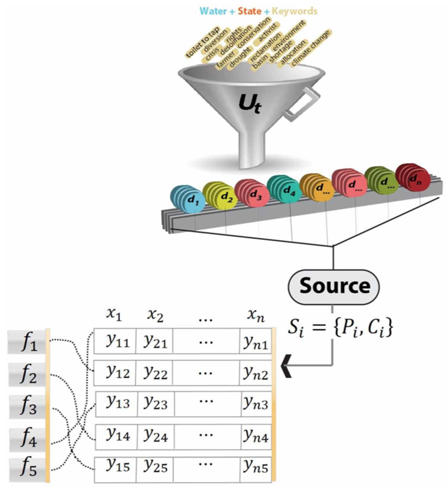
Framing involves using strategic devices for presenting prominent aspects and perspectives about an issue. Public opinion, attitudes, beliefs, and behaviors can be influenced by how an issue is framed. Our group explored the use of machine learning algorithms and mathematical techniques for Internet-scale data mining and semantic discovery of news content to enable the ability to mine, analyze, and visualize large-scale datasets. We focused on discovering how news articles on the topic of water insecurity in the Southwest United States are framed using an automated method of identifying the frame type.