In antiquity, the task of the astronomer was ‘to invent hypotheses by which the phenomena will be saved (that is, accounted for).’ The principal examples in antiquity of attempts to transcend this limitation and produce physically real astronomical systems were the adaptation of Eudoxus’s system of homocentric spheres by Aristotle, and the Planetary Hypothesis of Ptolemy.
Aristotle’s nested system of 55 concentric spheres accounted, in a qualitative way, for the major planetary phenomena, but failed to predict accurately either the variation in the length of the retrograde motion or the observed variation in the size and brightness of the planets. A system which would predict these phenomena was that of Ptolemy’s Almagest.
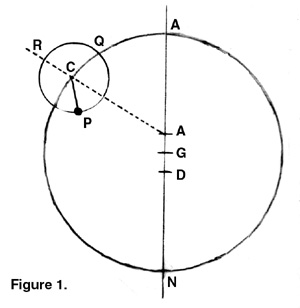
The Ptolemaic system relied on the A geometrical mechanisms of deferent, epicycle, and equant to transform uniform circular motion into the irregular motions of the planets. Ignoring variations in celestial latitude, one may describe the motions of most of the planets quite accurately by the diagram in Figure 1. The planet P revolves around the epicycle PQR at a constant velocity, while the center of the epicycle C revolves around the deferent circle CAN with a constant angular velocity with respect to the equant point E rather than either the center of the deferent G or the earth 0.
Reducing this system to a physical model was not difficult. Such a model consists of four spherical surfaces forming the boundaries between three regions. The surfaces S and S’ have the center of the universe, that is, the center of the earth O for their center, while T and T’ have the center of the deferent circle G as their center.
The planet P is embedded in a small sphere which is finally embedded in the spherical shell bounded by the surfaces T and T’, which in its turn is embedded in the sphere bounded by S and S’. The sphere between S and S’ shares the westward diurnal rotation of the starry sphere. The sphere between T and T’ moves in an irregular manner so that C moves with constant angular velocity around E and the small sphere moves with the velocity formerly attributed to the epicycle.
The Ptolemaic system in this form is accurate, but it is less satisfying than Aristotle’s system of homocentric spheres as each planet is moved by many spheres having diverse motions around diverse centers. A further attempt to establish a system of homocentric spheres was undertaken in the 12th century by a number of Spanish Arab philosophers and most fully elaborated by al-Bitruji.

The model of al-Bitruji, like that of Aristotle, N produces the complex motions of the planets by nested series of concentric spheres. The M poles of these three spheres are inclined at
appropriate angles to trace out the path of each planet. The outermost sphere shares the diurnal motion of the stellar sphere, rotating once daily around its axis NS which passes
through the poles of the earth and perpendicular to the equator WBE. This sphere carries around C with it the axis MR of the second sphere, which is inclined approximately 23° to the poles, a value constant for all the planets and equal to the obliquity of the ecliptic ABC. The second sphere rotates at a varying rate, approximately equal to the mean daily motion
of the planet through the zodiac and carries around with it the pole of the third sphere.
The axis LQ of the third sphere, which carries the planet P, is inclined to the second at an angle equal to the greatest deviation in latitude of the planet from the plane of the ecliptic.
This sphere, like the second, rotates at a varying velocity so computed that the rotation of the second and third spheres together produce the observed proper motion of the planet from
West to East through the zodiac, while the rotation of the third sphere produces the observed motion in celestial latitude.
From an astronomical point of view, al-Bitruji’s model had little to offer. It was incapable of yielding astronomical predictions without the introduction of a complex computation of the nonuniform motions of the second and third spheres. In fact, no known astronomical tables were based on this attempt at a physically real planetary system.