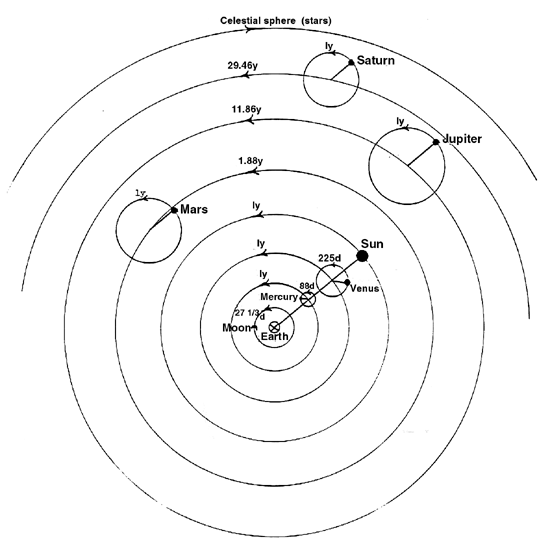
This diagram represents a simplified version of the Ptolemaic planetary model. It makes no attempt to illustrate relative sizes, distances, or centers of motion. For all that, it clearly shows several basic features seldom mentioned in 20th-century textbooks. First, note the ‘sun- linked motions’ of Mercury and Venus. Here Ptolemy imagined the center of the epicycles to move on an imaginary line connecting Earth and the Sun, the size of their epicycles account for their maximum elongation (Mercury, 29 degrees, Venus, 47 degrees). By the early decades of the 17th century a growing cosmological concern would not only be the apparent size and brightness of planets but their shape. Second, note that the geometrical line connecting Earth and the Sun runs parallel to the radius vectors connecting the center of each epicycle to each planet. I call this an ‘amazing parallel’. Third, a final feature to note is the repetition of a one-year (365 day) period in each planetary element. The deferent circle for the inferior planets is one year just as the epicyclic period for each superior planet is one year. But now the reader should be wary. Things always look simple in hindsight. It is too easy to ask how someone as ingenious as Ptolemy failed to explain (our word) the sun-linked motions of Mercury and Venus and the tantalizing implications of his ‘amazing parallels’ and ‘unexplained uniformities’. It is easy to speculate. Is it possible Ptolemy was not threatened by these symmetries, that on the contrary, like his bi-section of the eccentricity, Ptolemy saw these uniformities as theoretical justification for his views? Larger historical questions quickly arise. When does symmetry justify a fact? When does the relation of facts suggest something more than a description? What kinds of symmetry are most compelling? What is the relation between factual description and causal explanation?