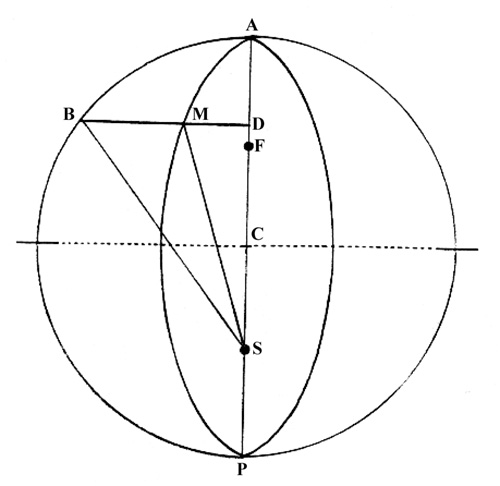
Kepler’s Problem can be described as follows. In this diagram, AMP is an ellipse, ABP a circumscribed circle, S and F are foci, A and P the aphelion and perihelion, and M the planetary position. For any planetary position (M) on an ellipse, the time taken to move from A to M is to the planet’s period as sector ASM is to the area of the ellipse. In order to simplify calculating area ASM, Kepler constructed BMD perpendicular to AP so that sector ASM is to the area of the ellipse as sector ASB is to the area of the circle, thus, SM and SB sweep our equal areas in equal times. As Kepler lamented, however, there is no directly calculable relationship between sector ASM and angle ASM or between sector ASB and angle ASB. As a result, Kepler was forced to rely on trial and error methods of approximation. In identifying the scope and difficulty of the problem, Kepler urged geometers to find a direct solution. As a result, it was thereafter known as Kepler’s Problem, and was taken up by several mathematicians, especially after the middle of the century when Kepler’s works became better known.