Robert Hatch

SUBTOPIC:

 Using an Historical Approach to Laboratory Work in the Style of Galileo

OBJECTIVES:

The students will:

1. make observations using 17th Century equipment and procedures
2. realize the importance of analyzing data accurately
3. develop an appreciation for how scientific knowledge was obtained in the 17th Century
4. use a model to visualize Galileo’s belief in the Copernican system by disproving the Ptolemaic system
5. be able to describe a projectile’s motion in terms of its vertical and horizontal components
6. learn how to demonstrate that the same acceleration of gravity exists on falling bodies as on projectiles
7. demonstrate the concept that the same gravitational force acts on any object
8. practice skills in measuring, recording, and graphing data, as well as making observations and inferences
9. realize that truth is not necessarily judged on observation alone, but is also influenced by well devised arguments and practical, although not always correct, common sense

Background Information

One of the most important concepts taught in any introductory course in physics is the development of the major ideas/inventions. A productive way of teaching such concepts is to have students actually perform experiments under conditions very similar to those in which the ideas developed. For example, the Project Physics lab, “A Seventeenth Century Experiment,” uses a simple grooved track and water clock to demonstrate the relation between distance travelled and time of a falling object. In performing this experiment, students follow Galileo’s assumption that a rolling ball’s speed increases just as a ball in free fall. Students also learn the basic graphical analysis as well as how to test the behavior of different sized balls on a ramp. Thus, the students succeed in comparing Aristotle’s belief with Galileo’s, and in contrasting the relationship between distances covered in equal time intervals.

Performing these experiments not only successfully reinforces the historical development of important inventions and ideas, but also aids in the development of the student’s reasoning skills. 

Galileo, born on February 15, 1564, was the son of Vincenzio Galilei, a cloth merchant and musician. Unlike Nicolas Copernicus and Tycho Brahe, Galileo was a second-generation intellectual. His father sent him to the local university to study medicine. Because Galileo had three sisters and a brother, his father could not afford to keep him in the university, so Galileo applied for a scholarship. He was surprisingly turned down, although he had already demonstrated brilliance. But Galileo continued his studies and invented mechanical instruments and wrote manuscripts. Because of this work, his brother-in-law was able to gain an appointment for Galileo as a lecturer at the University of Pisa, the same university that had previously turned him down. 
In 1592, Galileo became a professor of mathematics at the University of Padua. Here he remained for eighteen years and did his most creative work. Letters from Galileo’s early years gave evidence that he believed in the Copernican system. This system introduced three celestial motions:

1. rotation of the earth on its axis
2. the planets revolve around the sun
3. conical axial motion of the earth to explain a fixed earth’s orientation in space

Galileo was afraid to publish his opinions, not because of a fear of religious persecution, but rather a fear of being mocked and ridiculed. After the invention of the telescope (not invented by Galileo) and Galileo’s improvements to it, planets were seen which had not been seen before. The universe was becoming less and less perfect (ordered). After Galileo sought and received the Pope’s permission, he published The Messenger from the Stars (March 1610). In it he disclosed his observation of four new planets, the four moons of Jupiter. This disproved the main argument of the anti-Copernican followers that a planet orbiting another planet could not have orbiting moons. 

Galileo, at the age of forty-six, had finally published his belief in the Copernican system. Also stated in The Star Messenger was the observation that Venus goes through phases. This can not happen in the Ptolemaic Universe (see activity #l). Galileo also approached the problem of falling bodies. He abandoned the dynamic approach in favor of the kinematic approach. The study of the causes of motion is dynamics, while kinematics describes the positions and motions of objects. Aristotle said that velocity is proportional to force. When similar shaped spheres with different weights were dropped from the same height, they reached the ground at the same time. Galileo, on the other hand, said that velocity is proportional to time and that distance is proportional to time squared (see Activities 4 and 5). 

However, in 1616, the Holy Office decided that neither theory was acceptable and it not only banned Copernicus’s book, but told Galileo not to defend Copernicanism as well. Galileo went to Rome to persuade the Pope to allow him to continue to teach Copernicanism. He was told that he could speak of it only hypothetically. Galileo published his Dialogue, a three person argument in favor of Copernicanism. Once or twice Galileo even put some of the Pope’s own words into the character Simplicio’s mouth. The smartest of the three characters was a Copernican and the least intelligent (Simplicio) was anti-Copernican. 

Galileo was brought to trial and his Dialogue was banned. Hence, science virtually stopped in Italy and progressed in Northern Europe. Galileo was placed under house arrest and over the next five years, he went blind. Finally, at the age of seventy-eight, he died. 

ACTIVITY #1:

Heartbeats and Pendulums

          2 class periods

Background Information for Activity

While sitting in church one day, Galileo is said to have begun his analysis of the isochronism in motion of a pendulum by watching a censer swinging and timing it with his pulse. After completing the following timing experiment, similar to that of Galileo, students will understand the relationships between these variables in a pendulum: length, amplitude, mass and period.

PROCEDURE:

1. Have students pair up. One student is responsible for taking his/her own pulse, and the other is responsible for counting the swings of the pendulum.
2. Have students place their first two fingers gently over their carotid artery. They must concentrate until they get a feel for the rhythm of their heart beat. This will be used as a “timer” for recording the movement of the pendulum.
3. Set up the pendulum by using string and three equal masses. Tie one mass on one end of the string.
4. Next, tie the other end of the string on a support rod to make a pendulum 50 cm long.
5. Measure the length from the place where it swings to the center of the mass.
6. Set the pendulum swinging.
7. One partner must count ten complete full swings of the pendulum while the other partner makes a mark on a piece of paper for every pulse he/she feels. The goal is to concentrate on counting the pendulum swing while the partner marks down the number of beats until the 10 swings are up. The student counting his/her pulse should not look at the pendulum.
8. Count up the number of pulses. Repeat each time you want to time the pendulum.
9. Complete the following table:
   1. For columns A and B, use one mass, 10 cm amplitude (pull the pendulum 10 cm to one side), and vary the lengths starting at 50 cm. To calculate the period, divide the total number of heartbeats by the total number of swings (10). Put the answer in the data table below. If time allows, repeat this step and average the two values for the period before entering in column B.
   2. For columns C and D, use 50 cm length, amplitude 10 cm, vary the mass. Put the calculated periods into the table.
   3. For columns E and F, use 50 cm length, one mass, vary the amplitudes from 10 cm to 40 cm. Place the calculated periods into table.
      
A B C D E F

Length Period Mass Period Amplitude Period

(cm) (beats) (units) (beats) (cm) (beats)

50 1 10

40 2 20

30 3 30

20 4 40

10 5

10. Have students answer the following questions:
    1. How does the period change when the length changes?b) How does the period change when the mass changes?
    2. How does the period change when the amplitude changes?
    3. Which variable is the important one affecting the period of a pendulum?
    4. Plot a graph of length as a function of time–that is “L” against “T” and determine the shape of the graph.
    5. Since the two variables are proportional to one another, a straight line is formed. Plot “L” against “T²” on a second graph.
    6. Determine the shape of the new graph line.
    7. Determine if “L” is proportional to “T,” or to T₂.”
    8. Determine the length of a pendulum which has a period of exactly one heart beat.
11. Now, have the students test their prediction.
12. Finally, students should calculate the slope of the graph and use it to write a formula for the relationship between length and period of a simple pendulum.

ACTIVITY #2:

Seeing is Believing

            1-2 class periods

Background Information for Activity

Historically, Galileo was not recognized as the inventor of the telescope, but rather as the man who seized upon a Dutch invention, improved the design, and demonstrated the practical usefulness of the device to the merchants of Venice in 1609. He hustled a group of businessmen and clergy to the top of the Campanile for a handsome demonstration of the powers of the instrument–powers which he improved from a three-fold magnification to a nine-fold magnification. Within three short months, he constructed a twenty-power telescope and turned it on the heavens (specifically the moon), the satellites of Jupiter, and the sun. 

Unlike modern refracting telescopes, in which images are inverted and reversed (upside down and backwards), the Galilean telescope produced an enlarged image which was erect and normal (right side up with left and right as usual). 

PROCEDURE:

1. Divide students into small groups and provide them with the following instructions:
   1. Select a convex lens and a concave lens from the assortment in the classroom.
   2. Draw a profile of each lens.
   3. Place the lenses side by side on a printed page from the textbook, convex on the left and concave on the right. From now on, enter notes and observation in two columns on the work sheet provided below.

      Convex Concave
       

      ---

      size of image
       
       

      ---

      position of image
       

   4. Slowly, move each lens away from the page and toward their eyes. As distance increases, look at other objects across the room, or out through a window. Enter new information in the table above.
   5. Time for a prediction! DO NOT DO ANYTHING WITH YOUR LENSES YET.

    

2. Have students answer the following questions:
   1. What would happen if you held the concave lens in front of the convex lens?
   2. What would be the effect on the image you see?
   3. What is YOUR OWN opinion?
   4. Include a sketch showing the arrangement of your eye, concave, and convex lens.
3. Next, have the students follow the second set of instructions:
   1. Devise a possible theory with your group’s ideas.
   2. Now, test the theory. Be patient while adjusting the locations of the two lenses in front of your eyes. Describe what you see with a simple sketch.
   3. Explain the surprising results by writing just YOUR explanation first.
   4. Try other arrangements and combinations of lenses in an attempt to produce the greatest possible magnification of the object.
   5. With the help of your teacher and textbook, try drawing ray diagrams to explain how a single concave lens, appropriately arranged, can produce a magnified image which is both right side up and normal.
   6. Research to discover what the limits of magnification are with a Galilean telescope and how the tube was designed so as to maximize the effective magnification of the image.

ACTIVITY #3:

The Models

             45 minutes 

MATERIALS:

 TACKS, PINS, SCISSORS, STRING, WIRE, RULERS, GLUE, TAPE, CONSTRUCTION PAPER, MARKERS, DIAGRAMS OF THE PTOLEMAIC SCHEME AND THE COPERNICAN SCHEME (INCLUDED)

PROCEDURE:

1. Using an overhead projector, handout of the diagrams, or chalkboard, give a presentation and explanation of the Copernican and Ptolemaic systems (see attached diagrams).
2. Students, in groups, should design a model illustrating the Ptolemaic Universe, paying special attention to the fact that Venus, as seen from the earth, can not go through phases.

ACTIVITY #4:

Slowing Down Motion

             45 Minutes

MATERIALS:

 RAMP, STEEL BALL BEARING, PLASTIC RULER, METER STICK, CARBON PAPER, WHITE PAPER, TAPE

Background Information for Activity

Measuring the motion of a freely falling object is difficult because the speed constantly increases. Galileo slowed down the motion by using inclined planes, which makes things “fall” at an angle. 

PROCEDURE:

1. Divide a sheet of white paper into 10 equal parts by drawing vertical parallel lines. Draw one horizontal line approximately two inches from the top (this line should be perpendicular to the vertical lines).
2. Tape the paper to the ramp (with a small incline) with the vertical lines running up the ramp. Roll the ball bearing down the ruler so that when it leaves the ruler, it is traveling along the horizontal line. Note that it crosses each vertical line in equal time periods.
3. Repeat the process, placing carbon paper over the lined sheet, so that a path of the ball bearing will be recorded on the paper. The horizontal distance covered divided by the number of lines (which represents time) is always a constant. The vertical distance covered divided by the number of lines squared is always constant. The activity can be repeated for various inclines.

ACTIVITY #5:

Galileo: Falling Objects!

            1 class period

PROCEDURE:

1. Select work groups. Each group will be responsible for one of the following procedures:
   1. dropping an object and measuring the distances
   2. keeping time (using stop watches)
   3. recording data/calculations (all work should be completed before the class)
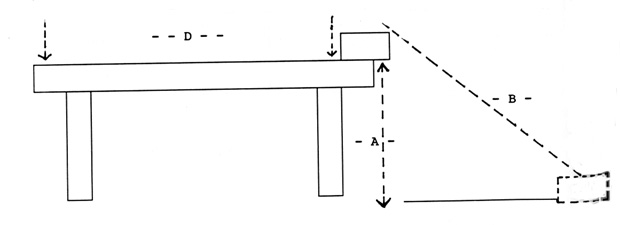
2. Drop an object from the table and measure the time that it takes for it to reach the floor.

   Hint: Repeat the procedure several times, rotating people in the work groups so as to get more involvement and increase accuracy. Also, the photoelectric probes included with many software programs are a wonderful supplement to your measurements.

3. Raise the level of the table to double the height, if possible, and repeat the measurement.

   Hint: you may want to raise the table in increments and use the data to calculate the average velocity of the object as the height changes:

   V = D/T

4. Record the data on the chart below:
   
Trial Distance Object Falls Time To Reach The Floor


5. Average the time for each height attempt for comparison to the results of activity 2.

Activity #6:

Observing the Fall of an Object Moving Horizontally

           1 class period

PROCEDURE:

1. Select work groups. Each will be responsible for completing the following procedures:
   1. measuring/pushing the object
   2. keeping time (using stop watches)
   3. recording data/calculations
2. Push the object the length of the table and let it fall off the table to the floor (repeat the process and deliberately vary the force used to push the object).
   
Data Chart

-A- -B- -C- -D- 

Attempt Distance Time to Length Avg. Velocity 

Off Floor hit floor from table On Table Top 

- - D - - 

- B -

- A - 

___________________ 

3. Increase the height of the table using exactly the same increments you used in activity #1. Continue to record the data in the chart prepared earlier.
4. Average the time (column B) it takes the object to hit the floor and compare to the results of activity #1.
   
Data Chart

Avg. 

Velo- 

city 

Distance from table


ACTIVITY #7:

Science and Culture: The Trial of Galileo
Acting out the Prosecution

             Advanced planning time of 1-2 periods and homework of 1 week. The performance of the trial is 1 period

MATERIALS: 

BOOKS ON THE HISTORICAL EVENT AND ON THE HISTORY OF ASTRONOMY AND PHYSICS, STAR CHARTS, STAR GLOBE, HOMEMADE 
                               EPICYCLE MACHINES, POSTER BOARD, MARKERS, COSTUMES (OPTIONAL)

Background Information for Activity

Galileo Galilei was an Italian scholar who was put on trial by the inquisition in 1644 AD for holding heretical opinions about the universe. At issue was the new Copernican world view championed by Galileo as contrasted to the Ptolemaic that had been accepted by the church for centuries as the correct and only model. The Copernican model was a sun centered system while the Ptolemaic system was earth centered. Galileo was judged guilty by the tribunal and his works were banned. The structuring of knowledge to conform to the wishes of society by legal or authoritarian means continues to present times (i.e. Scopes train, Oppenheimer and Lysenko affair).

The quotations included below are the responses given when asked to make a one sentence summarization of Galileo Galilei as a historical figure in science.

Richard Ernst, Oak Hill Private School–Physics:

“Galileo’s greatest contribution to science was the discovery of a new physics that enabled the mechanics of motion, and by extension the whole of nature, to be accurately described in terms of mathematics.”

Fran Earle, Youngstown High School–Chemistry:

“Galileo was a flamboyant scientist who studied laws of motion is such a way that he challenged the Catholic church by making earth (man) the center of the universe, for which he was imprisoned for life.”

Dr. Frederick Gregory, University of Florida–History of Science:

“Above all, Galileo was dogmatic, but it may have been his stubbornness that carried him through the legitimate objections of those who accused him of doing bad science.”

Todd Dixon, Palatka High School–History/Government:

“Galileo was a popular propagandist who attempted to popularize a theory in a time when those in power opposed this theory regardless of the truth.”

Walter Schroeder, Berkley Prep. School–History:

“Galileo, as a spokesman and as a symbol, defended the proposition that the essential nature of the spiritual is truth and that God is magnificently manifested in the natural world and its laws.”

Dan Van Gorp, Lake Weir Middle School–History:

“The original scientific patron-saint; the Adam of yuppiedom as a prostitute for inquiry.”

George Dewey, Chantilly HS–Physics:

“Galileo showed us consequences of a courageous distrust of authority and the naive belief that truth would alone persuade in science as in life.”

Dr. Robert A. Hatch, University of Florida–History of Science:

“Galileo transformed the medieval science of motion, cast Aristotelian philosophy into doubt, pointed the way in observational astronomy, and has since become a symbol (however misunderstood) of freedom of thought as a ‘right-thinking’ martyr.”

Chris Beckmann, Oak Hall School–History/Philosophy:

“Galileo the myth is often confused with Galileo the man: the myth invented the telescope, bravely challenged the great power of the church of Rome, and dropped objects down from the leaning tower of Pisa, while the man pinched the telescope from the Dutch, immediately recanted his ideas when shown the inquisition’s torture machines, and was, in end too old to climb the steps of Pisa’s tower.”

Note: This lesson plan works particularly well if the history and physics teachers combine their efforts to prepare the class.

PROCEDURE:

1. Choose a student (with confidence and sportsmanship) to play the part of Galileo.
2. Prepare the student by giving careful instructions on what to expect during the trial.
3. Send the student out of the room.
4. Prepare the rest of the class to form the prosecution by utilizing epicycle machines and celestial globes, as well as emphasizing the Ptolemaic model.
5. Choose several very persuasive students to serve as prosecutors.
6. The teacher may serve as the judge.
7. Bring in the accused.
8. Have the prosecutors present their case.
9. Allow Galileo to defend himself.
10. Have the jury determine the verdict.

*Suggestion: You may wish to involve other classes, such as younger children who have few preconceptions, to serve as a jury. Also, depending on how well your students can handle this unstructured activity, you may wish to incorporate a script of some kind, or have the students write out scripts or outlines themselves.

Bibliography

Boorstin, D.J. The Discoverers. New York: Random House, 1983. 

Bronowski, J. The Ascent of Man. “The Starry Messenger and the Maestic Clockwork.” Boston: Little Brown, 1973 

Casper, B. M. “Galileo and the Fall of Aristotle: A Case of Historical Injustice?” American Journal of Physics 45 (1977): 325.

Crowe, M.J. Theories of the World from Ptolemy to Copernicus. Chap. 4, 6, 8. New York: Dover, Inc.

Gingerich, 0. “Copernicus and Tycho.” Scientific America December 1973. 86. 

Koestler, A. The Watershed. Chap. 8. U P of America. 170-210.

Marks, J. Science and the Making of the Modern World. Heinemann Educational Books, 1988. 

The Project Physics Course. Chapt. 7. New York: Holt, Rinehart and Winston, Inc., 1970.

Dugan. Famous Physical Scientist.