Collaborators: Dylan Small, Paul Rosenbaum, Xinran Li, Ruth Heller, Ben French, S. Siddarth, Gourab Mukherjee, Zheng Wang, Megan Ennes, Bhuvanesh Pareek, Pulak Ghosh, Indranil Mukhopadhyay, Chyke Doubeni, Doug Corley, Marshall Joffe, Ann Zauber, Wreeto Kar, Anqi Zhao, Youjin Lee, Ruoqi Yu, Bodhi Sen and others. I am extremely grateful to all my collaborators.

Research has been generously supported by current and past grants: NSF-DMS­ 2015250 (PI), NIH/NCI 5R01CA213645­-05 (Co-I), NIH/NIA 1R21AG065621­-01A1 (Co-I), and NIH/NINDS 1R01NS12112-0­01 (Co-I).

In causal inference from observational data, biases can and do replicate. Thus, a causal effect that is consistent across several studies does not provide any greater confidence regarding a true causal effect. Neither does a treatment effect estimate with a small statistical error. But, we can strengthen the evidence for a causal effect if multiple nearly independent analyses for the causal hypothesis where the analyses depend on assumptions that do not completely overlap, provide supportive evidence. This is because neither bias nor statistical error that might invalidate one piece of the evidence can invalidate supportive evidence from others. Thus, evidence for a causal effect is strengthened if multiple evidence factors provide support for a causal effect, and such evidence is further robust to a moderate degree of unmeasured confounding in different directions. In this line of research, my colleagues and I develop statistical methods for the design and analysis of evidence factors in observational studies.

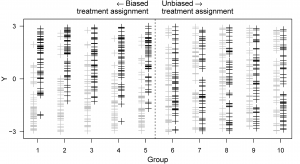
Recently, we have developed a new ‘two-point’ identification strategy for the causal effect of a treatment subject to unmeasured confounding. The method is based on the insight of the following figure: In the unbiased groups, these two sets of points mix with each other; in fact, their theoretical variances are equal. Compared to this common variance, the variabilities of the points within both the treated and controls seem smaller in the biased groups because these groups prefer the treatment when outcomes are higher.

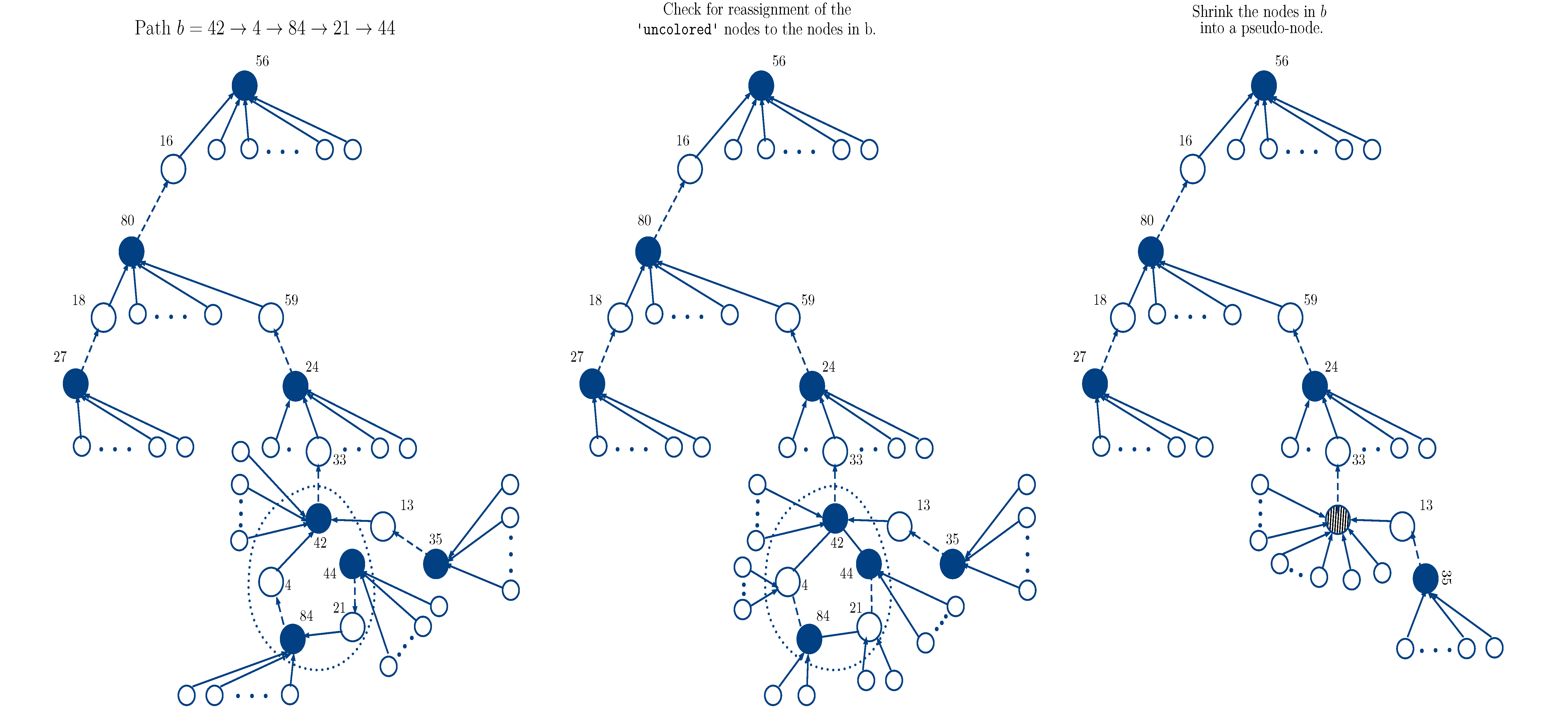
A careful analysis of an observational study requires planning and design. Traditional treatment-control analysis of an observational study needs little planning and a simple matched pair design. More sophisticated analyses that attempt to get more out of an observational study require additional planning and designing. We need new computer algorithms to create these designs. Most of these design problems, e.g., balanced blocking and balanced reinforcement, are NP-hard, i.e., they cannot be guaranteed to be solved in a reasonable time for every instance of the problem. In this line of research, my colleagues and I develop and implement approximation algorithms that run fast, guarantee an upper bound on the possible error it can make in the worst case, and perform close to optimal in a typical case.

Modern marketing problems pose new statistical challenges. I develop spatial and longitudinal statistical models and inference methods that aim to gain a better understanding of how consumers adopt new products during the product’s different life-cycle and demonstrate how manufacturers can leverage the revealed heterogeneous contiguity effects to develop more effective targeted promotions to accelerate the consumer adoption of the product.

In an observational panel study, units are observed over time, where a subset of the units are exposed to the treatment at some time during the study period. Thus, panel studies provide opportunities to learn about the treatment effect over time. Additionally, from the methodological point of view, panel studies hold an additional benefit in that causal conclusions can be drawn even when the ignorability assumption fails to hold. Methods such as difference-in-differences or two-way fixed effects models have been part of empirical researchers’ toolbox for a long time. Their ease of use has catapulted their popularity. However, recent literature has emphasized that causal inference from these methods relies on crucial assumptions. When these assumptions fail, these methods can result in severely biased inferences. In this line of research, I aim to develop new statistical methods for these types of challenging cases in panel studies where the existing methods fail.