Alexander Wagner

Embeddings of Persistence Diagrams into Hilbert Spaces
Peter Bubenik and Alexander Wagner
Abstract: Since persistence diagrams do not admit an inner product structure, a map into a Hilbert space is needed in order to use kernel methods. It is natural to ask if such maps necessarily distort the metric on persistence diagrams. We show that persistence diagrams with the bottleneck distance do not even admit a coarse embedding into a Hilbert space. As part of our proof, we show that any separable, bounded metric space isometrically embeds into the space of persistence diagrams with the bottleneck distance. As corollaries, we obtain the generalized roundness, negative type, and asymptotic dimension of this space. [arXiv]

Nonembeddability of Persistence Diagrams with p > 2 Wasserstein Metric
Alexander Wagner
Abstract: Persistence diagrams do not admit an inner product structure compatible with any Wasserstein metric. Hence, when applying kernel methods to persistence diagrams, the underlying feature map necessarily causes distortion. We prove persistence diagrams with the p-Wasserstein metric do not admit a coarse embedding into a Hilbert space when p > 2. [arXiv]

Stabilizing the Unstable Output of Persistent Homology Computations
Paul Bendich, Peter Bubenik, and Alexander Wagner
Abstract: We propose a general technique for extracting a larger set of stable information from persistent homology computations than is currently done. The persistent homology algorithm is usually viewed as a procedure which starts with a filtered complex and ends with a persistence diagram. This procedure is stable (at least to certain types of perturbations of the input). This justifies the use of the diagram as a signature of the input, and the use of features derived from it in statistics and machine learning. However, these computations also produce other information of great interest to practitioners that is unfortunately unstable. For example, each point in the diagram corresponds to a simplex whose addition in the filtration results in the birth of the corresponding persistent homology class, but this correspondence is unstable. In addition, the persistence diagram is not stable with respect to other procedures that are employed in practice, such as thresholding a point cloud by density. We recast these problems as real-valued functions which are discontinuous but measurable, and then observe that convolving such a function with a suitable function produces a Lipschitz function. The resulting stable function can be estimated by perturbing the input and averaging the output. We illustrate this approach with a number of examples, including a stable localization of a persistent homology generator from brain imaging data. [arXiv]

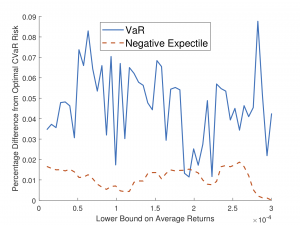
Portfolio Optimization With Expectile And Omega Functions
Alexander Wagner and Stan Uryasev
Abstract: This paper proves equivalences of portfolio optimization problems with negative expectile and omega ratio. We derive subgradients for the negative expectile as a function of the portfolio from a known dual representation of expectile and general theory about subgradients of risk measures. We also give an elementary derivation of the gradient of negative expectile under some assumptions and provide an example where negative expectile is demonstrably not differentiable. We conducted a case study and solved portfolio optimization problems with negative expectile objective and constraint (code and data are posted on the web). [arXiv]