I work in the field of Topological Data Analysis (TDA) and I am part of Dr. Bubenik’s research group in the Department of Mathematics at the University of Florida. TDA is a new branch of mathematics and some theoretical foundational work is still required. I wish to continue developing theoretical aspects of TDA. I believe many classical mathematical theories have yet to find their applications in data science problems. In particular, I am interested in using applied sheaf theory in advancing ideas in TDA. I am also using old ideas by Eduard Čech about Čech closure spaces, a generalization of topological spaces. I am also collaborating with the Vitriol Lab and using TDA and machine learning algorithms to analyze the actin cytoskeleton of cells that have undergone some perturbations.
I have also mentored undergraduate students in Peter Bubenik’s research group:
- David Freeman, analysis of microscopic cell images using relative persistent homology
induced by quotient and shortest path metric. - Gianfranco Cortes, training a support vector regression model to distinguish between types
of singularities in algebraic varieties.
More detailed descriptions of the above mentioned projects are given below:
Homological Algebra for Persistence Modules
A preprint of this work is available at https://arxiv.org/abs/1905.05744.
In TDA, we often start with data that was processed to obtain a diagram of topological spaces, such as a filtered cubical or simplicial complex. Applying a homology  functor with field coefficients we obtain a diagram of vector spaces.Such a diagram is called a persistence modules and in applications this object decomposes as a direct sum of indecomposables thanks to a theorem by Gabriel.
functor with field coefficients we obtain a diagram of vector spaces.Such a diagram is called a persistence modules and in applications this object decomposes as a direct sum of indecomposables thanks to a theorem by Gabriel.
In this project, together with Peter Bubenik, I developed some aspects of the homological algebra of persistence modules, in both the one-parameter and multi-parameter settings, considered as either sheaves or graded modules. I showed the two theories are different. I considered the graded module and sheaf tensor product and Hom bifunctors as well as their derived functors, Tor and Ext, and gave explicit computations for interval modules. I gave a classification of injective, projective, and flat interval modules. I stated Kunneth theorems and universal coefficient theorems for the homology and cohomology of complexes of persistence modules in both the sheaf and graded modules settings and showed how these theorems can be applied to persistence modules arising from filtered cell complexes. I also gave a Gabriel-Popescu theorem for persistence modules. Finally, I examined categories enriched over persistence modules. I showed that the graded module point of view produces a closed symmetric monoidal category that is enriched over itself.
Topological Data Analysis of Actin Networks
A poster of this work is available here.
 This is a data analysis project with Peter Bubenik, Parker Edwards and collaborator Dr. Eric Vitriol and his PhD student Kristen Skruber from the College of Medicine at the University of Florida. We consider high-resolution microscopy images of live cells. Networks of filaments assembled from the actin family of proteins contribute significantly to cells’ ability to move and change shape. These actin networks exhibit distinct local geometric structure. Some networks contain regions of straight and tightly packed fibers, for instance, as well as loops of varying sizes. Our data consist of microscopy images of cells which visualize the actin cytoskeleton fibers. Our methodology detects localized features using image segmentation and tools from topological data analysis: subsampling and relative persistent homology, persistence landscapes and support vector regression. Some classes of cells have a gene knocked out and some are given drugs, modifying the geometry of the cells’ actin networks. Using geometric summaries of patches covering each image together with machine learning algorithms, we produce a score and a visualization for each image that both quantifies the actin cytoskeleton and allows practitioners to interpret the results in terms of the structurally diverse regions in the cell.
This is a data analysis project with Peter Bubenik, Parker Edwards and collaborator Dr. Eric Vitriol and his PhD student Kristen Skruber from the College of Medicine at the University of Florida. We consider high-resolution microscopy images of live cells. Networks of filaments assembled from the actin family of proteins contribute significantly to cells’ ability to move and change shape. These actin networks exhibit distinct local geometric structure. Some networks contain regions of straight and tightly packed fibers, for instance, as well as loops of varying sizes. Our data consist of microscopy images of cells which visualize the actin cytoskeleton fibers. Our methodology detects localized features using image segmentation and tools from topological data analysis: subsampling and relative persistent homology, persistence landscapes and support vector regression. Some classes of cells have a gene knocked out and some are given drugs, modifying the geometry of the cells’ actin networks. Using geometric summaries of patches covering each image together with machine learning algorithms, we produce a score and a visualization for each image that both quantifies the actin cytoskeleton and allows practitioners to interpret the results in terms of the structurally diverse regions in the cell.
Convolution of Persistence Modules
A preprint of this work is available at https://arxiv.org/abs/2010.02020.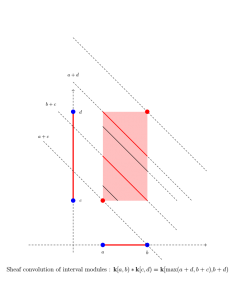
Sheaves and cosheaves have found many applications in data science problems of the local-to-global character. A common perspective in applications is to study sheaves and cosheaves on partially ordered sets often valued in vector spaces over a field. The thesis work of Justin Curry showed that functors from a partially ordered set into a “nice” category are equivalent to sheaves and cosheaves on open and closed sets of the Alexandrov topology on the partially ordered set, respectively, valued in said category. An example of this are cellular sheaves and cosheaves. On an arbitrary topological space sheaf cohomology is well defined and studied in the derived setting for any sheaf. On the other hand, cosheaf homology is only defined for constant or locally constant cosheaves. However, on finite partially ordered sets one can construct a rich sheaf cohomology andcosheaf homology theory in the framework of derived functors for any sheaf and cosheaf. One can even study entropy and information theory from this point of view.
This project is analogous in spirit to the work by Kashiwara and Schapira for bounded derived complexes of constructible sheaves. It turns out that persistence modules themselves are both sheaves and cosheaves on R with the Alexandrov topology. I define sheaf and cosheaf convolution operations for bounded derived complexes of persistence modules. I define a convolution distance on the bounded derived category of (multiparameter) persistence modules. I show this distance extends the classical interleaving distance of persistence modules. I prove stability results for this distance. I show that the convolution of cosheaves is canonically isomorphic to the derived graded module tensor product operation. I also show the cosheaf convolution has a right adjoint. This adjunction is analogous to the Tamarkin-Kashiwara-Schapira adjunction for constructible sheaves.
Foundations of Algebraic Pretopology
I am undertaking a systematic study of a new approach to topological data analysis (TDA) using old ideas of Eduard Čech. Together with Peter Bubenik, I study Čech closure spaces, also called pretopological spaces, via a modernized approach that is in harmony with the viewpoint of categorical homotopy theory. Čech closure spaces have recently seen use in analyzing connectivity and proximity relations in chemical spaces and modeling chemical reactions and biological evolutionary processes.As closure spaces are good at modeling proximity relations they can be used in data science for example in text mining, complex network analysis, structure analysis, classification and clustering.
I consider constructions on data that produce a diagram in which each object has the same underlying set — the data — but in which the underlying closure structure (pretopology) changes. The morphisms in this diagrams are identities on the underlying set but in which the closure structure becomes coarser. I think of these as localizations, which increase the scale at which we consider the data. Indeed, if fixing a probe to study our data and considering maps from the probe into the diagram, as the closure structures become coarser the set of maps from the probe increases. In some sense, the objects remain fixed but there are more morphisms. By suitable choices of probes and applying standard functors we obtain interesting diagrams of simplicial sets, simplicial abelian groups, chain complexes, homology groups, and homotopy groups, which provide information on the underlying data. I show that this general approach recovers numerous previously-defined constructions, such as the discrete homology of metric spaces and graphs, cubical and simplicial homologies of digital images, the Vietoris Rips homology groups of finite metric spaces and the recently developed path homology for simple directed graphs. I state and prove theorems for closure spaces analogous to classical ones from algebraic topology, e.g. Mayer-Vietors, Excision, Hurewicz etc.
Combinatorial Applications of Computational Geometry and Algebraic Topology
I have been accepted to be a part of the AMS mathematical research community (MRC) on Combinatorial Applications of Computational Geometry and Algebraic Topology. This research will be centered around the new, rapidly expanding field of Analytic Combinatorics in Several Variables (ACSV), which concerns itself with enumeration problems in such areas as lattice walks, statistical mechanical models, quantum walks and other exactly solvable models where asymptotic estimation of coefficients of a bivariate or multivariate generating function is required. The multivariate setting allows for the consideration of mathematical problems coming from singularity theory, algebraic topology, and computational algebra. Solving problems from these areas of mathematics has direct applications to ACSV. A long-term goal is to advance and automate this work, so that its benefits can be used by other researchers in mathematics and the natural sciences through implementations in computer algebra packages. We will consult problems in effective computer algebra methods, algorithms using computational topology, multivariate asymptotic phase transitions, singular transforms for degenerate saddle-point integrals, and applications of harmonic analysis and singularity theory.