The focus of my research is to develop new tools for analyzing data, to understand their underlying mathematical theory, and to use these tools in applications. This work lies in the field of applied topology, and more specifically, topological data analysis.
Why is topological data analysis of interest to data scientists?
Topological data analysis (TDA) approaches data science with a toolbox based on ideas from algebraic topology which are very different from the ideas underlying standard approaches to data analysis. It is particularly useful in situations where the data has a complex structure that is crucial to understanding the data but is sufficiently complicated that we are unable to construct a satisfactory model using standard methods.
Why is topological data analysis of interest to mathematicians?
TDA has important and beautiful connections with a wide variety of mathematics. My current research uses results from probability, combinatorics, functional analysis, representation theory, commutative algebra, geometric topology, general topology and category theory. It is exciting to explore new connections between pure mathematics and applications.
What is applied topology and topological data analysis?
Algebraic topology is particularly useful for connecting local and global properties of mathematical objects. Often the local description is easy to understand, but one is particularly interested in global qualities that depend on how the local information fits together. Many powerful tools in algebraic topology have been developed for this purpose. Applied topology adapts these tools so that they may be used for the same purpose in an applied setting.
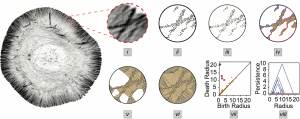In topological data analysis, data is encoded in an increasing sequence of complexes. This choice of encoding requires a good understanding of both the data and the topological machinery. Persistent homology provides an efficient algorithm for calculating and describing how the topology of this complex changes as one moves along this sequence. One then uses this summary make inferences on the data.