On this page I have a number of items to get the interested reader started with persistent homology and topological data analysis (TDA).
My resources
I’ve written the following to help beginners get started with Topological Data Analysis.
Worksheets
To learn the basic definitions and constructions, complete the following.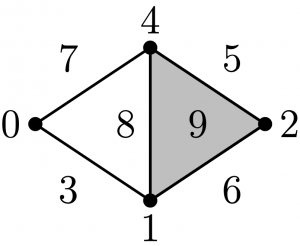
Topological Data Analysis with R
If you want to get started doing topological data analysis, complete the following.
To see the output of these scripts, view the following PDFs.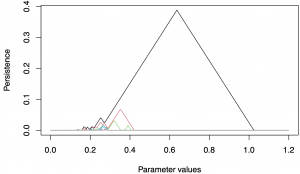
Other resources
If you know linear algebra you are ready to start! If you you’ve never heard of linear algebra, you can still learn what TDA is about with this article on TDA and Pokemon
- Connecting the Dots: Discovering the “Shape” of Data, by Michelle Feng, Abigail Hickok, Yacoub H. Kureh, Mason A. Porter, and Chad M. Topaz.
Introduction to Topological Data Analysis and Persistent Homology
- Introduction to Persistent Homology, a great YouTube video, by Matthew Wright
- Studying the Shape of Data Using Topology, a brief non-technical introduction by Michael Lesnick
- A User’s Guide to Topological Data Analysis, by Elizabeth Munch.
- Persistent homology: an introduction via interactive examples, by Federico Iuricich.
- Introductory Topological Data Analysis, by Dayten Sheffar.
Simplicial Homology
The main technical tool for persistent homology is simplicial homology. For persistent homology, we use coefficients in a field. So simplicial k-chains are vectors and the set of simplicial k-chains is a vector space. Furthermore, the boundary map is a linear transformation. For finite simplices, it is represented by a matrix.
Topological Data Analysis and Persistent Homology
Here are some recent introductory articles. If you want to learn more about the subject I would recommend starting here. The first three are mathematical, the fourth emphasizes connections to data science, and the fifth is more statistical.
- A Brief History of Persistence, by Jose Perea
- Persistent Homology and Applied Homotopy Theory, by Gunnar Carlsson
- Homological Algebra and Data, by Robert Ghrist
- An introduction to Topological Data Analysis: fundamental and practical aspects for data scientists, by Frédéric Chazal and Bertrand Michel
- Topological Data Analysis, by Larry Wasserman
There is a Wikipedia page.
The following slightly older introductory articles provide background, some mathematical details and a few applications.
- Persistent Homology – Theory and Practice, by Herbert Edelsbrunner and Dmitriy Morozov
- Barcodes: The persistent topology of data, by Robert Ghrist
- Topology and data, by Gunnar Carlsson
-
Topological pattern recognition for point cloud data, by Gunnar Carlsson
The following are more technical summaries of some of the main results in the field.
- Persistent Homology, by Herbert Edelsbrunner and Dmitriy Morozov
- High Dimensional Topological Data Analysis, by Frederic Chazal
Books
For a mathematics graduate student wanting to learn the subject, I highly recommend starting with reading Part 1 of the following book. Those interested in applications to biology should also read Part 2.
- Topological Data Analysis for Genomic and Evolution, by Raul Rabadan and Andrew Blumberg
I also recommend the following books.
- Computational Topology for Data Analysis, by Tamal Dey and Yusu Wang
- Persistence Theory: From Quiver Representations to Data Analysis, by Steve Oudot
- Topological Data Analysis with Applications, by Gunnar Carlsson and Mikael Vejdemo-Johansson
Topological Data Analysis and Deep Learning
- PLLay: Efficient Topological Layer based on Persistence Landscapes, by Kwangho Kim, Jisu Kim, Manzil Zaheer, Joon Sik Kim, Frederic Chazal, Larry Wasserman.